Logo Header

Vibration Transmission Calculation



Understanding Vibration Transmission Loss in a Mass-Spring System


Calculating the Transmission Loss on a single Mass-Spring Sytem


The Vibration Transmission Loss for a one degree of freedom system is calculated by modeling it as a damped mass-spring system. The ratio between the exciting force and the transmitted force is given by the following formula:

\[ T = \left| \frac{F'}{F} \right| = \left[ \frac{1 + \left( \frac{2 \xi \omega}{\omega_0} \right)^2}{\left( 1 - \left( \frac{\omega}{\omega_0} \right)^2 \right)^2 + \left( 2 \xi \frac{\omega}{\omega_0} \right)^2} \right]^\frac{1}{2} \]

Calculating the Resonance Frequency a damped system


The resonance frequency (fp) in Hz is calculated considering a damped system as shown below:

\[ f_p = f_0 \sqrt{1 - 2\xi^2} \]

where:


Calculating the Transmission Loss on a Double Mass-Spring Sytem


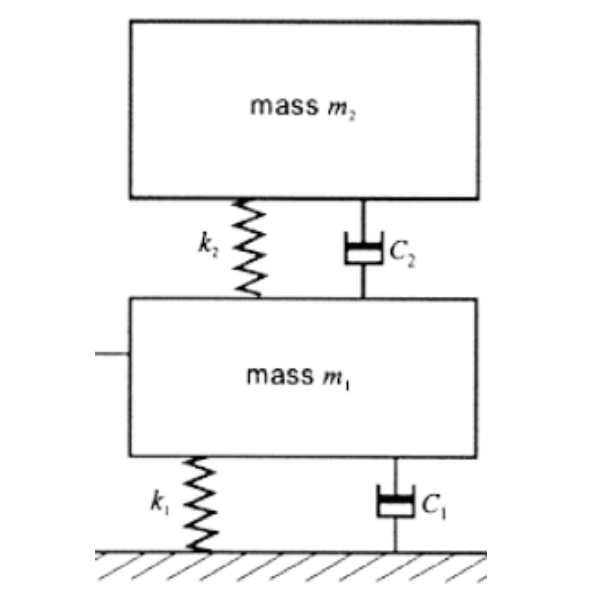
In the double suspension system, the model consists of two masses and two springs connected to a rigid ground. The calculation of the transmissibility is derived from Bies - Engineering Noise Control Theory and Practice using the following formula:

\[ T = \frac{(k_1 + j\omega C_1)(k_2 + j\omega C_2)}{(k_1 + k_2 - \omega^2 m_1 + j\omega C_1)(k_2 - \omega^2 m_2 + j\omega C_2) - (k_2 + j\omega C_2)^2} \]

where:

The indices 1 and 2 refer to the components of the system, with index 1 representing the mass, stiffness, and damping connected to the ground, and index 2 representing the mass, stiffness, and damping above system 1.

Diagram of a double suspension vibration system used for calculating vibration transmissibility

The two resonant frequencies are calculated using the method outlined in Harris' Shock and Vibration Handbook - Fifth Edition, P1.10.

For more detailed information, read our article on effective vibration reduction strategies.



Footer