Vibration : Strategies for effective reduction

Introduction

Machines are everywhere in our life.

In factory, lot of machines are used to produce our equipment. In transport like train or car, motors and other rotating machines helps us everyday to move.

Most of these machines produce efforts and these latter generate vibration in their attachment structure.

Impact of vibration

These vibrations have adverse impacts from causing a discomfort by making noise (structure borne noise) or vibration with an influence on our health and well-being. When the vibrations are high, it could even be damageable for the machine or other equipment around it implying costs in the maintenance or a reduction of the lifespan.

For these reasons, the reduction of the vibrations are an important aspect to take into account in the designing of a machine.

But how to do it?

Play on the source

As generally in engineering, the most effective way is to play with the source. Less the source generates efforts, less vibrations are. In this article, we will not try to solve it because otherwise, we will need an article for each types of machine. Generally, the equipment supplier makes studies to design its product. For example, for an electrical motor, a study of the interaction between electromagnetic forces and the vibro-acoustic responses of the equipment structure are performed by the supplier.

The art of the disconnection

In the case where it’s not possible to change the source, one of the main solutions is to modify the interface between the machine and the receiving structure.

It could be done by 2 ways (or 3):

• Add a soft element between the machine and the structure
• Change the stiffness of the structure
• Or the both

The first common solution is to place a decoupling at the interface. We can schema the complete equipment with the decoupling as a “spring-mass” system.

A spring-mass system is the simplest representation of a mechanical design.

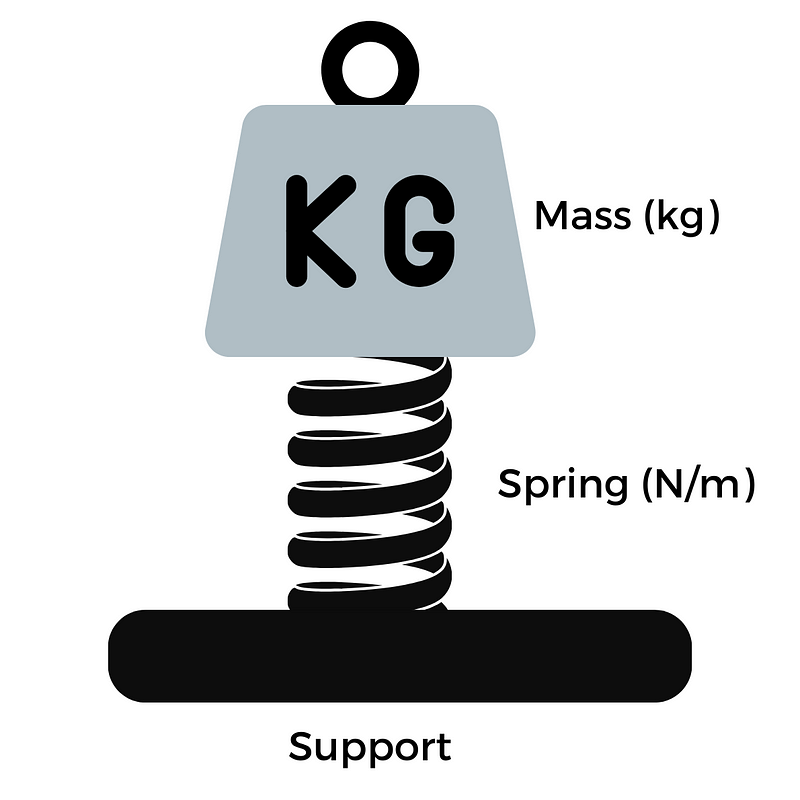
The main characteristic of this system is the resonance frequency (Hz) that depends of the weight of the “mass” (kg) and the stiffness of the “spring” (N/m).

But what happen at this resonance frequency?

If you excite the mass with an effort at this frequency (fr — red zone), the effort transmitted will be amplified. Below this frequency (<fr — blue zone) the amplification is close to 1 (no amplification, no reduction) and after this frequency (>fr — vibration reduction), the force will be reduced. This ratio, between the force transmitted and the force of the machine is called Transmissibility.

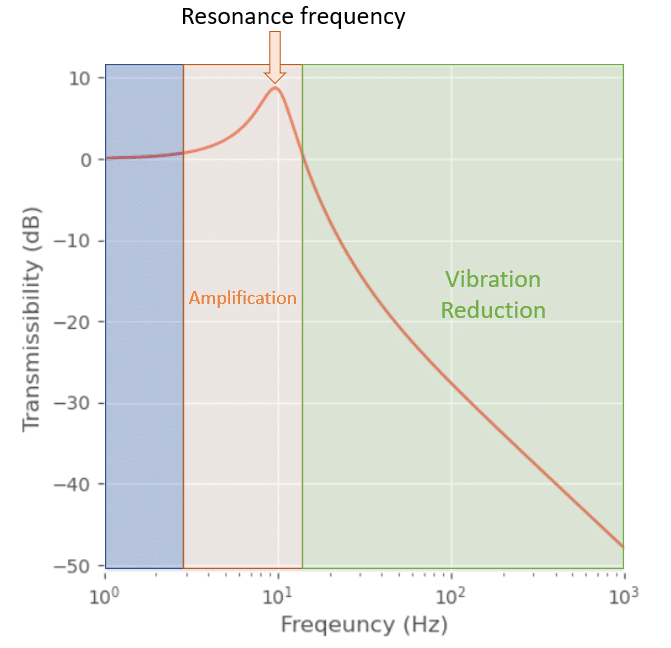
As you can imagine, the job here is to design the “spring” in order to have the transmissibility lower than 1 (and even less).

OK, so we know the behavior of a basic mass-spring system with, before the resonance frequency no amplification, at the resonance, amplification (depending of the damping) and after the resonance reduction of forces.

To complete our analysis, we need also another input data. Indeed, if the system is not excited, no forces so no vibration, of course. We need to know the characteristics of the machine to determine the different excitation frequencies.

If the excitation frequencies are close to the resonance frequency, as we have seen before, the forces will be amplified and therefore the vibration too. We must avoid this case and try to have the excitation frequencies far from the resonance (more than a ratio of 2)

So now, we have almost all the elements to design our decoupling. We know :

• The excitation frequencies of the machine
• With the mass of the machine, we can calculate the good spring to have a resonance frequency far from the excitation (at least 2 times lower the excitation frequency)

That s all?

Unhopefully, the real world is a little bit complicated than a simple mass-spring system.

The first thing is that a machine mounted on soft spring has 6 degrees of freedom (translational and rotational). This means at least 6 possible resonance frequencies to take into account with sometimes different stiffness of the silent block depending of its shape (important to have the stiffness in all directions).

Moreover, the stiffness of a silent block depends of the type solicitation. Basically, to have the static stiffness, a measurement of the displacement in function of applied force is done. But in dynamic, the material behavior is different. For example, for elastomeric silent block, there is a rigidification when the material is sollcited dynamically. It implies that the dynamic stiffness is around 1.5–2 higher than the static stiffness (and more in some frequencies), giving an increasing of the resonance frequency. For steel spring, this could be checked with the supplier and the damping is generally low.

A chewing gum on another chewing gum?

The last but not least, the silent block must be attached at a support, a structure.

This structure has also a mass and a stiffness, therefore it should have a sufficient stiffness to not “facilitate” the propagation of the vibration. Imagine you push with your fingers on the silent block and the structure move too. It will be certainly problematic for the vibration.

As first approximation, a ratio of 10 between the stiffness of the silent bloc and the structure is correct. Of course, this comparison could be done in static (as first approximation) but above all in dynamic thanks to a structure measurement with accelerometer and impact hammer. It enables too to see the influence of the modes of the structure and it s better to avoid a coupling between excitation frequencies and these modes.

This rule is also applicable when the machine has not silent block. Indeed, an important stiffness or a low mobility (ratio acceleration/force) could limit the propagation of the vibration.

Another way to reduce the resonance frequency is to modify the mass of the system by mount the machine directly on a massive block that will be decoupled.

Two better than one?

After reading all of that, we could imagineadding 2 or more silent blocks in series to improve the reduction of the vibration.

It’s a good idea but…

To come back to our simple mass-spring system, if there are 2 stages silent blocks (with a frame between), we will have a “mass-spring-mass-spring”. Argh!

This implies more resonance frequencies and sure, the transmissibility will be lower than only one stage. But you imagine that it’s necessary to check all the possible coincidences between all resonance frequencies (in all directions) but with also with the excitations frequencies. A nightmare!

It doesn’t mean to not use it, but it should be designed carefully. This configuration could be useful for a machine mounted on a frame with other auxiliaries machine on this frame (that is decoupled from another structure)

All is perfect?

As all solutions, decoupling have some limits.

• Vibration of the machine : The first one is that the discoupled machine will have more vibration itself so you must check with the supplier, the vibration level acceptable on the machine.
• Environment constraints and life duration : Moreover and especially for elastomeric support, they are sensible to the temperature (and other environment constraints) and the life cycle is often less than the machine itself so it’necessary to forecast a replacement every a couple of years.
• Max loads : For machine mounted on vehicle, it s important to design stops to avoid to loose your equipment on the road. Sometimes these stops are integrated in the silent blocks or shall be designed and placed on the structure. To know how to design the stops, you must take into account the max forces, the weight of the machine and the stiffness of the silent blocks. With that, it s possible to calculate the max displacement and the efforts transmitted to the stops.
• Variable regime: A machine with variable regime has an infinite excitation frequencies so it s difficult to design easily the silent blocks. In this case, it s important to study the behaviour of the machine, probably there are some regimes more frequent than others and to find the best strategy to limit the time where the regime cross the resonant frequencies. Adding more damping could help too to limit the amplitude at the resonance.
• Weight repatition : it s not really a limit but if the weight of the machine is not equivalent on all supports, it s important to design different silent blocks. Moreover, if one silent blocks are overloaded, it can get out of the functionning point and the silent block will be more rigid.
• Parasitic connexion : we must carefully pay attention to the connection between the machine with the other part of the system. It could make a short-circuit and reduce the efficiency of the silent blocks. So soft ducts (or to discouple) shall be designed to avoid that.

In conclusion

We have seen the different aspects to reduce vibration from a machine with silent blocks. To sum up, it requests to perform a global study including the checking of all the excitation frequencies and resonance of the system but also all other constraints (environment, shocks, vibration limit requirements,…).

I hope this article will help you and to know more do not hesitate to comment🙂

Thank you!