Logo Header
🎧 Last places to learn acoustic and vibration in May 2025, France - Discover our training plan (French language) More details

Double Wall Resonance Calculator

mass spring mass image



Double Wall Resonance Frequency Calculation


What is the double wall resonance frequency of a double wall


The resonance frequency of a double wall refers to the specific frequency at which the system formed by two parallel walls and the cavity between them naturally amplifies vibrations.

This phenomenon occurs when the dynamic interaction between the mass of the walls and the stiffness of the air (or material) in the cavity behaves like a mass-spring-mass system.

At resonance, the acoustic insulation of the wall system significantly decreases, allowing sound to pass through more easily.

Identifying this frequency is crucial in building acoustics to design wall assemblies that minimize sound transmission, especially in the frequency ranges of human speech or mechanical equipment.

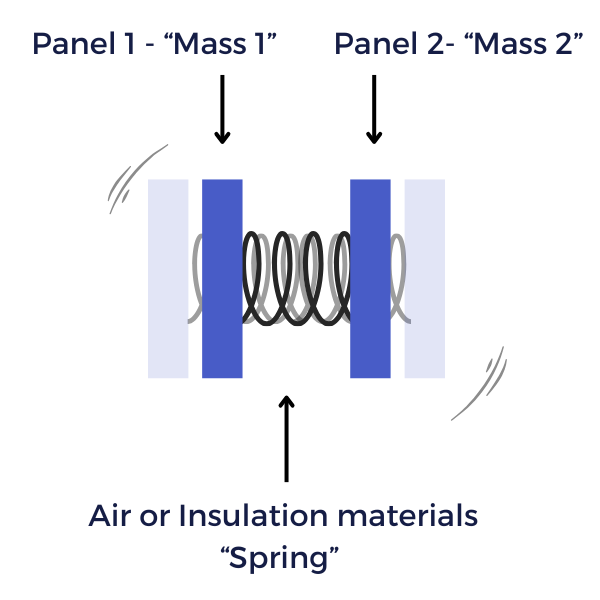
Diagram of the mass-spring-mass model used in double wall resonance analysis
Figure : Schematic of the Mass-Spring-Mass acoustic system

How to calculate the resonance frequency of a double wall


The resonance frequency of a double wall system is calculated using the mass-spring-mass model. In this model, the cavity acts as the spring, and each wall is treated as a lump mass. The formula used to calculate the resonance frequency is:

\[ f_{\text{msm}} = \frac{1}{2\pi} \sqrt{\frac{s'_g}{\frac{\rho_{s1} \rho_{s2}}{\rho_{s1} + \rho_{s2}}}} \]

Where:

  • \( s'_g \) is the dynamic stiffness per unit surface of the gas, measured in \( \frac{N}{m^3} \)
  • \( \rho_{si} \) is the mass per unit surface of material \( i \), measured in \( N/m² \)

Dynamic Stiffness Formula


The dynamic stiffness \( s'_g \) is calculated using the formula:

\[ s'_g = \frac{\gamma P_0}{L_z} = \frac{\rho_0 c_0^2}{L_z} \]

Where:

  • \( \gamma \) is the specific heat ratio, equal to 1.4 for air in adiabatic compression, and 1 if the cavity is filled with fiber materials due to heat conduction by the fibers.
  • \( P_0 \) is the atmospheric pressure, and \( L_z \) is the cavity depth.
  • \( \rho_0 \) is the air density, and \( c_0 \) is the speed of sound in air.

Dynamic Stiffness of resilient material


For the dynamic stifness of the resilient material when it's linked to the 2 panels (like sandwich material or underlayer screed), the dynamic stiffness could be measured using the ISO 29052. Some equipment like ImpAcTool could be used to measure it.


The measure of the dynamic stiffnes consist to create a mass-spring system with the specimen to test acting as spring and a steel plate (200kg/m²) as the mass. By applying a force (hammer or shaker), we obtain the resonant frequency of the system and could calculate the dynamic stifness of tha material

Reference: Sound Insulation - Carl Hopkins

And to calculate the complete transmission loss of materials, use AcouVApp Insul

Footer