The Science Behind Double Wall Acoustic Insulation

When it comes to acoustic insulation, the notion that "double walls work wonders" might seem like old news to some. However, delve a bit deeper, and you'll discover that this field harbors intriguing complexities and nuances. As we'll see, the efficacy of double-wall systems in soundproofing is not just about adding layers but understanding the intricate dance between materials, air gaps, and frequencies.

The Basic Principle: Beyond the Single Material

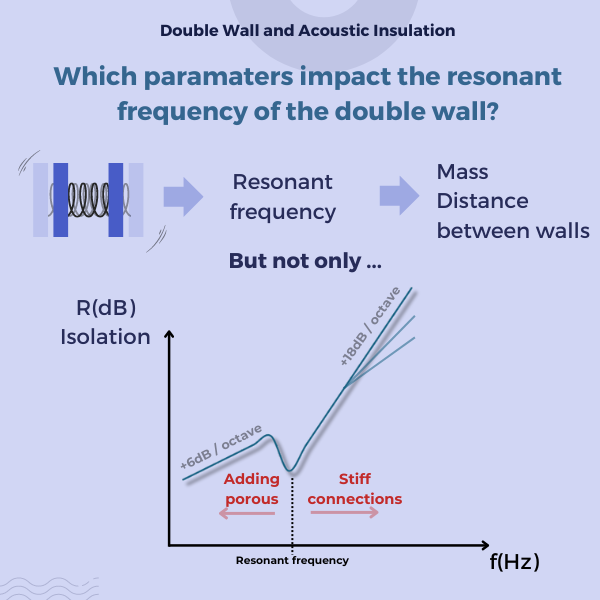
The conventional wisdom holds that a double-wall system—comprising two separate materials with an intervening air gap—vastly outperforms a single homogenous material in sound insulation. The reason behind this is fascinating: such a configuration can result in an acoustic insulation improvement of up to 18dB when doubling the frequency, a stark contrast to the 6dB improvement offered by a single-wall (mono-wall) system.
However, this remarkable performance boost is contingent upon surpassing the resonance frequency of the mass-spring-mass system that the double-wall constitutes. This is where things start to get a bit more complex.

For information the double wall frequency in Hz is calculated considering a mass-spring-mass system. The cavity has the role of spring and each wall as a lump mass. The formula used is :

• \( s'_g \) the dynamic stiffness by unit surface of the gas \( \frac{N}{m^3} \) - We will see later the calculation
• \( \rho_si \) the mass per unit surface of the material i (N/m²)

The Critical Role of Resonance Frequency

Understanding the resonance frequency is crucial in designing double-wall systems. This frequency depends on the mass of the materials and the thickness of the air gap. Simplistically, increasing the air gap or the mass of the materials lowers this frequency. Knowing the resonance frequency, calculated from mass and distance between panels, seems straightforward—yet it's not always that simple.

The Complexity of Materials

1. The Porous Material Factor

Introducing porous materials into the cavity introduces the first major complication. With an "empty" cavity, the stiffness of the air is calculated assuming adiabatic compression (no heat exchange), leading to a specific heat ratio ("gamma") of 1.4. This assumption falls apart when a porous material is added. The heat exchange with the porous material's fibers means the system becomes isothermal, changing "gamma" to 1. This adjustment affects the stiffness of the air gap and shifts the resonance frequency by about a third of an octave [1].

This gamma appears in the formula of \( s'_g \): $$s'_g = \frac{\gamma P_0}{L_z} = \frac{\rho_0 c_0^2}{L_z} $$ with :

• \( \gamma\) the Specific Heat Ratio that is equal to 1.4 in air in adiabatic compression and 1 in the case where the cavity is filled with fiber materials due to heat conduction by the fibres

2. The Stiffness of Connections

The second complication arises from the stiffness of connections between the panels. For flexible connections, resonance frequency calculations generally hold up. However, with stiffer connections (like thick steel studs or wooden structures), a mechanical interaction alters the boundary conditions of the panels, as if they were fixed. The result? The resonance frequency can double for stiff wooden connections [2][3].

The Implications

Adding porous materials tends to lower the resonance frequency, while stiffening the connections increases it. These insights demonstrate the delicate balance required in calculating the acoustic insulation of double-wall systems—a task that demands a thorough understanding of the system's components and their interactions.

In Conclusion

The science of acoustic insulation, especially regarding double-wall systems, unveils a realm where materials, air, and sound interact in complex ways. The effectiveness of such systems in soundproofing transcends mere material addition, venturing into the realm of precise, informed design and engineering. This realm is guided by a deep understanding of how sound waves interact with structures, necessitating a nuanced approach to achieve optimal results. As the field advances, the promise of quieter, more serene spaces becomes increasingly attainable, underscoring the fascinating interplay between physics, materials science, and architectural design.

Thank you for your reading!

References

• [1]Carl Hopkins-Sound Insulation
• [2]Davy-2019-Structural connections and the sound insulation of cavity walls
• [3]Davy-2019-Empirical corrections for predicting the sound insulation of double leaf cavity stud building elements with stiffer studs