Understanding Critical Frequencies in Acoustic Isolation

Introduction

In the realm of acoustic isolation, encountering a dip in performance at certain frequencies can be critical. This phenomenon occurs due to the presence of characteristic frequencies, notably critical frequencies and coincidences.

What are Critical Frequencies?

At critical frequencies, the transmission of sound through a material is at its peak, resulting in a significant dip in acoustic isolation. This means less isolation and consequently, less comfort. But what exactly happens at these frequencies?

The Mechanism Behind It

Consider a simple plate. For a given angle, there is a specific frequency where coupling (or coincidence) occurs between the plate's bending waves and the acoustic wave. This happens when the wavelength projection of the sound matches the flexural wavelength of the plate, and the velocities of the acoustic waves and the bending waves in the material are equal. This leads to substantial acoustic radiation.

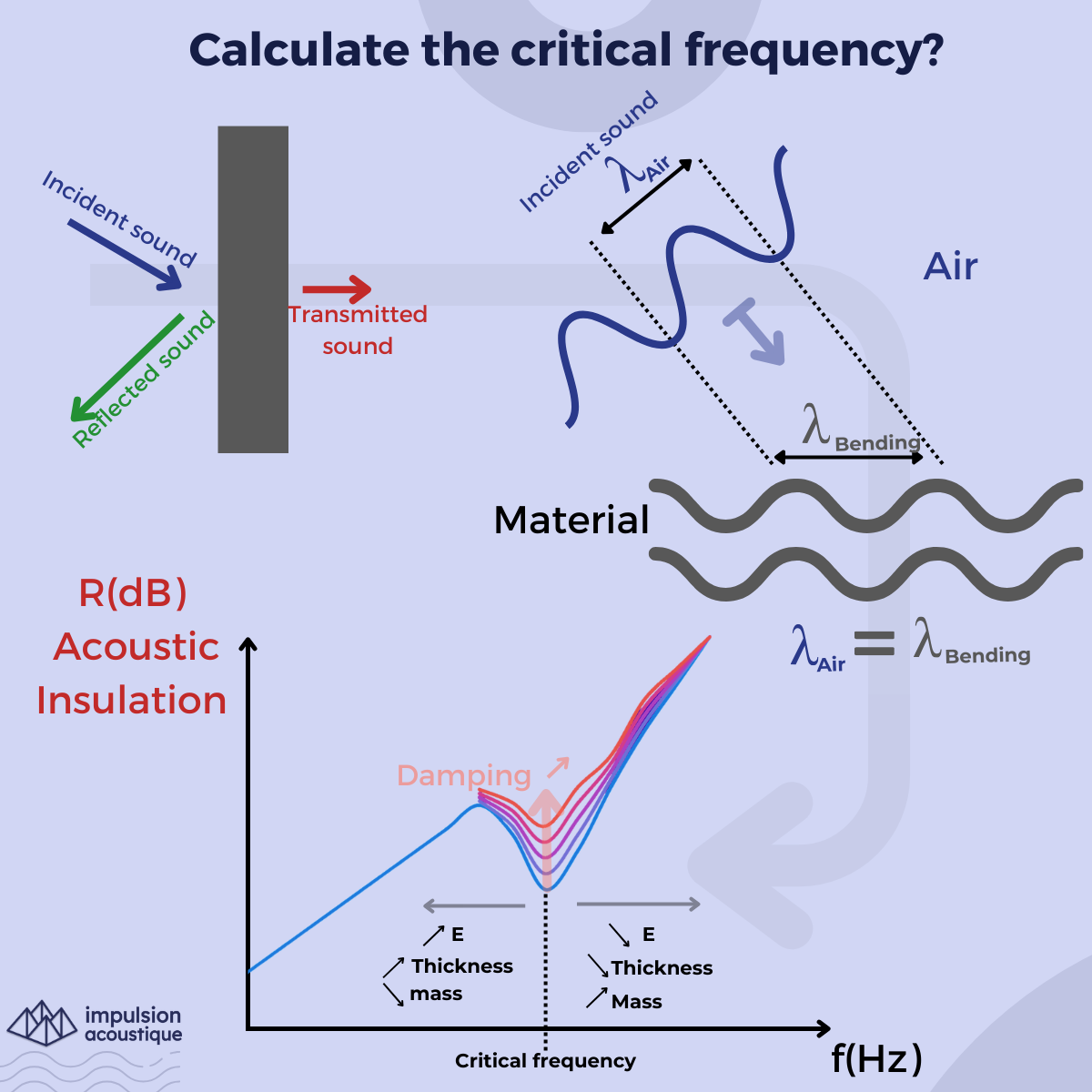
How to calculate it?

The Critical Frequency appears when the bending wavelength is equal to the acoustic wavelength (or the celerity of the bending wave is equal to the sound celerity) :
$$ f_c = \frac{c_0^2}{2\sqrt{\frac{\rho_s}{B_p}}} = \frac{c_0^3}{\sqrt{\pi}} \sqrt{\frac{3\rho_s(1-\nu^2)}{Eh^3}} $$ with :

• \( \rho_s \) the mass per square meter (m²)
• \( E \) the Young Modulus (Pa)
• \( \nu \) the Poisson Modulus
• \( h \) the thickness (m)
• \( c_0 \) the sound celerity (m/s)

Impact on Acoustic Isolation

These coincidences cause a loss in the isolation curve, which can be as severe as 10-15dB. Here are some characteristics of this critical frequency:

• Amplitude Control: The isolation amplitude at this frequency is controlled by the damping of the plate. This is why sandwich plates with viscoelastic layers or plates with damping materials are beneficial.
• Influencing Factors: The thickness, Young's modulus, and surface mass impact the position of this frequency. By adjusting these parameters, the critical frequency can be shifted to a less problematic range. For example, steel with a 2mm thickness has a critical frequency of 5500 Hz, while 4mm thick steel has a critical frequency of 2200 Hz.
• Directional Stiffness: Materials with different stiffness in different directions can exhibit multiple critical frequencies.
• System Design Considerations: When constructing a mass-spring-mass system, it's advisable to avoid plates with closely spaced critical frequencies to prevent the "kiss-cool" effect.
• Environmental Dependence: The critical frequency also depends on the environment in which the material is placed. THe critical frequencies will be not the same in the air and water

There are methods to calculate or estimate these frequencies based on material measurements, helping in designing better acoustic isolation solutions.

Understanding and managing these critical frequencies is essential for achieving optimal acoustic comfort in various applications.